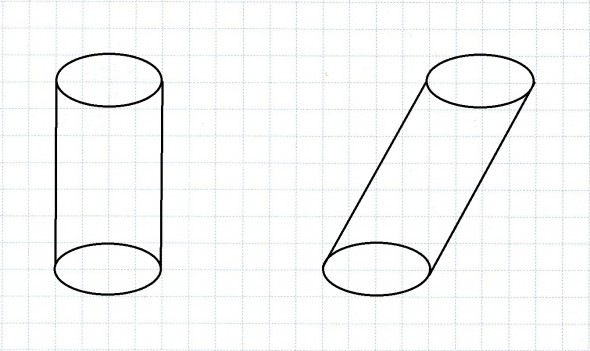
Silindir yüzeyini meydana getiren doğrulardan her birine ana doğru denir.
Hacim:
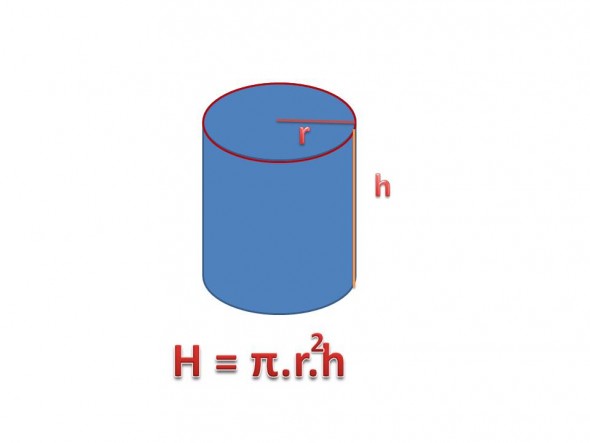
Hacmi: V=π.r2.h
π: 3,14 sabit sayı olarak alınır.
r2: (r kare) yarı çap demektir.
h: silindirin yüksekliği
H = taban alan.yükseklik
H = π.r.r.h
( π=3,14 alırız, r taban yarıçapı, h yükseklik )
Örnek:
Taban yarıçapı 4 cm ve yüksekliği 5 cm olan silindirin hacmini bulunuz. (π=3)
Cevap;
- r=4
- h=5
- v=?
(π=3) H= 3.4.4.5= 240 cm küp olarak bulunur.
Tekrar edecek olursak; Silindir o şekilde bir katıdır ki onun yan yüzeyi bir eğri yüzeydir.
Bu şekilde olan katı, herhangi bir yatay düzeyde yuvarlanabilir.
İşte bunun içindir ki ona silindir denmiştir.
Silindirde karşılıklı tabanlar paralel ve eşittir.
Bir silindirin yüksekliği, üst tabanından alt tabanına indirilen dikeydir.
Bir silindir, kenarının tabanlarına dikey veya eğik olduğuna göre dikey silindir veya eğik silindirdir.
Dikey silindir, bir dikey dörtgenin bir kenarı etrafında tam olarak dönmesiyle elde edilir.
Yüksekliği 0,80 m. ve tabanlarından her birinin çemberi 1,20 m. olan bir dikey silindir düşünelim.
Bu silindirin yan alanı 0,80 X 1,20= 0 96 mk. dir.
Bir silindirin yan yüzeyini yayarsak bir dikey dörtgen elde ederiz ki, bunun tabanı silindir tabanı çemberine ve yüksekliği de silindirin yüksekliğine eş olur .
Alan:
A = yanal alan + 2 taban alan
A = 2.π.r.h + 2.π.r.r
(π=3,14 alırız, r taban yarıçapı, h yükseklik)
Örnek:
Taban yarıçapı 1 cm ve yüksekliği 4 cm olan silindirin alanını bulunuz. (π=3)
A= 2.3.1.4+2.3.1.1= 24+6= 30cmkare








Leave feedback about this